为什么 0.1 + 0.2 不等于 0.3 ？为什么 16777216f 等于 16777217f ？为什么金钱计算都推荐用 decimal ？本文主要学习了解一下数字背后不为人知的存储秘密。

---

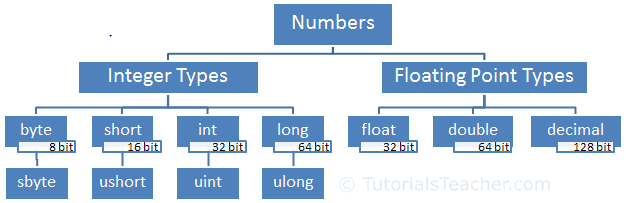
01、数值类型

C#中的数字类型主要包含两类，整数、小数，C#中的小数都为浮点（小）数。

void Main()
{
	int a1 = 100;
	int a2 = 0x0f; //15
	var b2 = 0b11; //3
	var x1 = 1;    //整数值默认为int
	var y1 = 1.1;  //小数值默认为double
	Add(1, 2.3); //3.3
	Add(1, 3);   //4
}
private T Add<T>(T x, T y) where T : INumber<T>
{
	return x + y * x;
}

• 用 var 类型推断时，整数值默认为 int ，小数值默认为 double 。
• .NET 7 新增的一个专门用来约束数字类型的接口 INumber <T> ，用来约束数字类型非常好用。

数值类型大多提供的成员：

?静态字段	说明
MaxValue	最大值常量， Console.WriteLine(int.MaxValue); //2147483647
MinValue	最小值常量
?静态方法	说明
Parse、TryParse	转换为数值类型，是比较常用的类型转换函数，参数 NumberStyles 可定义解析的数字格式
Max、Min	比较值的大小，返回最大、小的值， int.Max(1,100) //100
Abs	计算绝对值
IsInfinity	是否有效值，无穷值
IsInteger	是否整数
IsNaN	是否为NaN
IsPositive	是否零或正实数
IsNegative	是否表示负实数

数值类型还有很多接口，如加、减、乘、除的操作符接口，作为泛型约束条件使用还是挺不错的。

?操作符接口	说明
IAdditionOperators	加法
ISubtractionOperators	减法
IMultiplyOperators	乘法
IDivisionOperators	除法

public static T Power<T>(T v1, T v2) where T : INumber<T>,
	IMultiplyOperators<T, T, T>, IAdditionOperators<T, T, T>
{
	return v1 * v1 + v2 * v2;
}

---

02、小数、浮点数⁉

C#中的小数类型有float、double、decimal 都是浮点数，浮点 就是“ 浮动小数点位置 ”，小数位数不固定，小数部分、整数部分是共享数据存储空间的。相应的，自然也有 定点小数 ，固定小数位数，在很多数据库中有定点小数，C#中并没有。

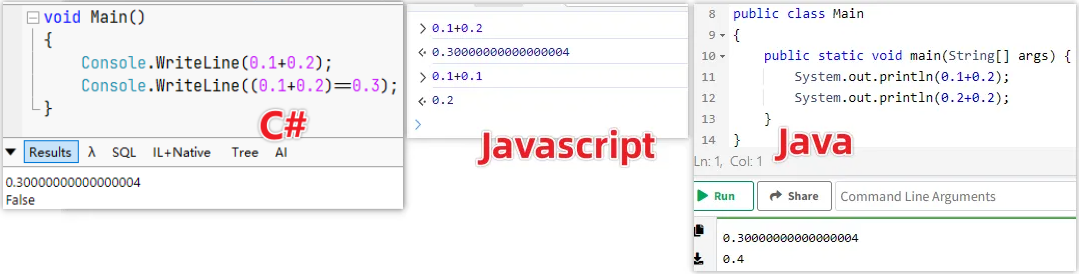
在编码中我们常用的浮点小数是float、double，经常会遇到精度问题，以及类似下面这些面试题。

• ❓ 为什么 0.1 + 0.2 不等于 0.3 ？
• ❓ 为什么浮点数无法准确的表示 0.1 ？
• ❓ 为什么 16777216f 等于 16777217f ？这里 f 表示为 float 。
• ❓ 为什么 32 位 float 可以最大表示 3.402823E38 ， 64 位 double 可以最大表示 1.79*E308 ，那么点位数根本存不下啊？
• ❓ 同样是32位， float 的数据范围远超 int ，为什么？

Console.WriteLine(0.1 + 0.2 == 0.3);       //False
Console.WriteLine(16777216f == 16777217f); //True
Console.WriteLine(double.MaxValue); //1.7976931348623157E+308
Console.WriteLine(int.MaxValue);    //2147483647
Console.WriteLine(Sizeof(double));  //8 //8字节（64位）

float、double为浮点数，小数位数有限，比较容易损失精度。造成上面这些问题的根本原因是其存储机制决定的，他们都遵循IEEE754格式规范，几乎所有编程语言和处理器都支持该规范，因此大多数编程语言都有类似的问题。Decimal 为高精度浮点数，存储机制与float、double不同，她采用十进制方式表示。

❗ 要搞懂float、double，就不得不了解IEEE754规范！

2.1、IEEE754：float、double存储原理

IEEE 754 （ 维基百科 ）是一个关于浮点数算术的国际标准，它定义了浮点数的表示格式、舍入规则、特殊值、浮点运算等规范。IEEE 754 标准最早发布与1985年，其中包括了四种精度规范，其中最常用的就两种： 单精度 （float，4字节32位）和 双精度 （double，8字节64位）。大多数编程语言、硬件处理器都支持这两种浮点数据类型，因此float、double的知识几乎是所有语言通用的，可以深入了解一下，不亏的！

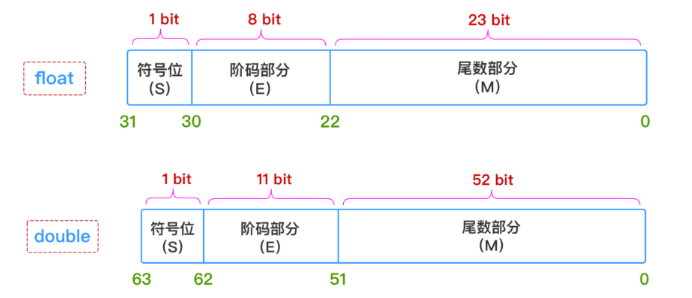
IEEE 754 浮点数不像十进制字面量值那样存储，而是用下面的二进制方式来表示并存储的，其实就是二进制的科学计数法。其二进制表示包含三个部分： 符号位S 、 指数部分 （阶码E，2为底的指数）和 尾数部分M 。

• ? 符号位（Sign） ：占用1位，这是浮点数的最高位，用于表示数字的正负。0表示正数，1表示负数。

• ? 指数部分（ExPONEnt，阶码） ：表示为2位底的指数，这里使用了移码，实际的指数 e = E-127 ，这样省去了指数的符号位，计算也更方便。

  • float 的指数部分8位， 2^8=256 偏移量（移码）为127，表示十进制范围为 [-127，128]，其数据范围就为 ±2^128 = ±3.4E38 。指数全是1即指数值为255时，表示为无效数字 ±infinity或NaN。
  • double 的指数部分11位， 2^11=2048 偏移量（移码）为1023，十进制值范围[-1023，1024]，因此数据范围 ±2^1024 = ±1.79E308 。

• ? 尾数部分（Mantissa） ：这部分表示数字的精确值（有效数字），包括整数和小数部分。尾数长度决定了精度，因为有效数字长度是有限的，因此就必然存在精度丢失的问题。

  • float 的尾数部分23位，十进制 2^23=8388608 ，最多6~7（不完整的第7位）位有效十进制数字，只有前6位是完整的。
  • double 尾数长度52位， 2^52 = 4503599627370496 ，因此最多有15~16 位有效十进制数字。

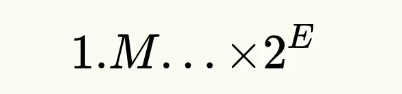
IEEE754浮点数都会被转换为上述二进制形式： **符号*尾数*2^指数** ，如 2 = 1.0 * 2^1 ， 0.5 = 1.0 * 2^-1 ， 5 = 1.25* 2^2 。数据（整数、小数部分）先转换为二进制形式，然后左移或右移小数点，转换为 1.M 形式，始终都是 “1”开头，因此就只存储小数部分即可。

?浮点数 =

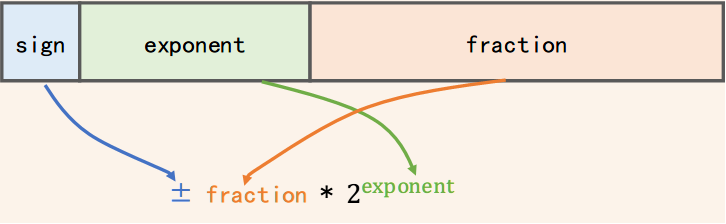
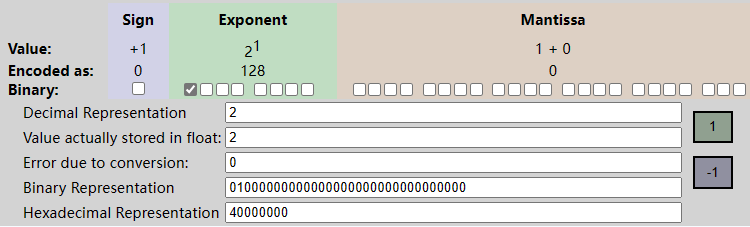
十进制 2 就表示为 2 = 1.0* 2^1 。下图来自 在线IEEE754转换器计算： IEEE-754 Floating Point Converter 。

• 阶码 E = 127+1 = 128 （实际指数e=1） 。
• 尾数 1.0 ，实际存储的尾数就是 0 。

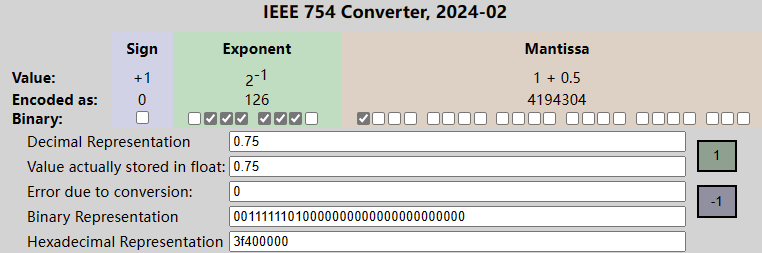
十进制 0.75 表示为 0.75 = 1.5* 2^-1 ，指数为 -1 ，尾数为 1.5 。

• 阶码 E = 127+ (-1) = 126 （实际指数e=-1） 。
• 尾数 1.5 ，实际存储的尾数就是 0.5 ，二进制值为 0.1 。为什么0.5 的二进制为0.1呢，请看后续章节。

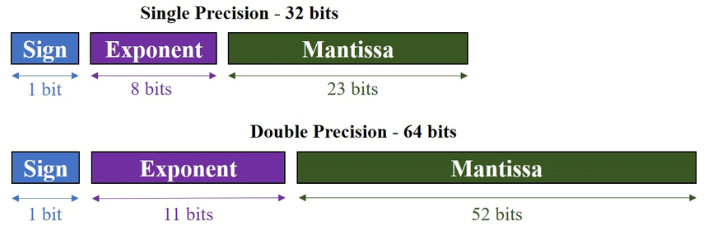
2.2、float、double对比

类型	单精度 float	双精度 double
CTS类型	System.Single	System.Double
长度	4字节32位	8字节64位
符号位S	1	1
阶码（指数位T）	8，[-127，128]	11，[-1023，1024]
尾数M	23	52
阶码偏移量	127， e= E -127	1023， e= E -1023
精度（10进制）	**6~7 **， 2^23=8388608	15~16 ， 2^52 = 4503599627370496
范围	±3.402823E38 ， 2^128=3.4E38	±1.79*E308， 2^1024=1.79E308
字面量表示（后缀）	f / F	d / D

float只能用于 表示6~7个有效数字时，才不会损失精度。

//7位有效数字
Console.WriteLine(4234567f);  //4234567
//第8位就不准确了
Console.WriteLine(42345678f); //42345680
Console.WriteLine(42345671f); //42345670

//7位有效数字
Console.WriteLine(0.2345678f);  //0.2345678
//第8位就不准确了
Console.WriteLine(2.12345678f); //2.1234567
Console.WriteLine(0.212345678f); //0.21234567

2.3、小数是怎么转换为二进制的？

对于整数转换小数是非常容易理解的，计算机的二进制是天然支持整数存储为二进制的。十进制整数转成二进制通常采用 ”除 2 取余，逆序排列” 即可。

Console.WriteLine($"{1:B4}"); //0001
Console.WriteLine($"{2:B4}"); //0010
Console.WriteLine($"{3:B4}"); //0011
Console.WriteLine($"{4:B4}"); //0100
Console.WriteLine($"{5:B4}"); //0101
Console.WriteLine($"{8:B4}"); //1000

?“B”格式只支持整数，更多格式化参考《 String字符串全面了解>字符串格式化大全 》

?乘2取整法

但小数则不同，采用的是 “ 乘2取整法 ”，小数部分循环迭代，直到小数部分 =0 为止。：如下 0.875 的十进制浮点数转换为二进制格式为： 0.111 。

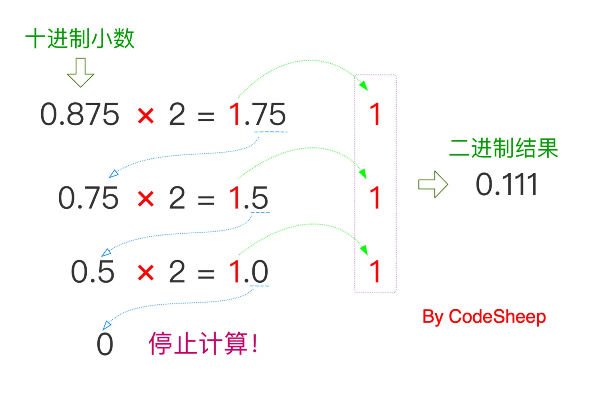
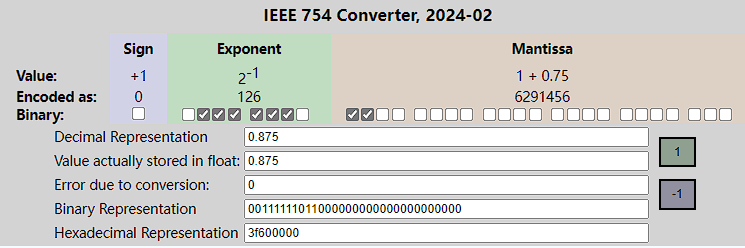
0.111 ，存储为IEE754浮点数，转换为 1.M*2^E 结构，小数点右移一位，就是 1.11*2^-1 。

• 指数E = -1 + 127 = 126 ，二进制值为 01111110 。
• 尾数为 11 后面补0。

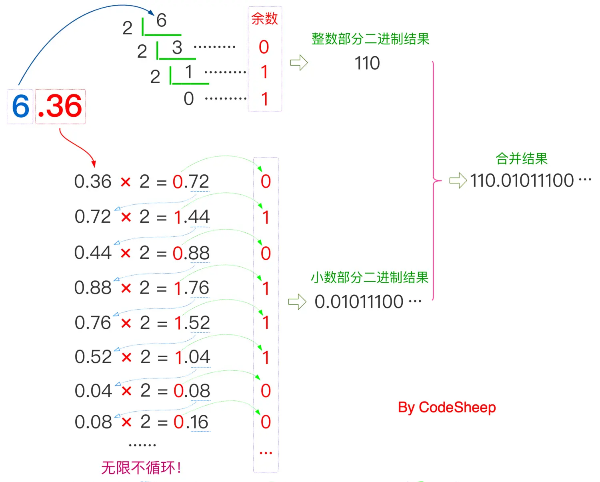
十进制小数 6.36 转换为二进制，整数部分+小数部分分别转换后合体：

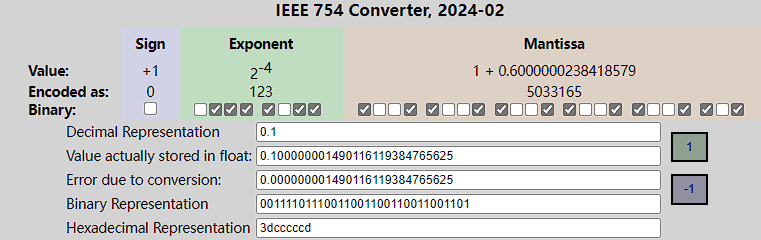
?无限循环的0.1！

二进制无法准确表示小数 0.1 ，是因为 0.1 转换为二进制后是无限循环的， 0.0 0011 0011 0011... ，“0011”无限循环。就像十进制小数 1/3 = 0.333 一样。

转换为 1.M*2^E 结构，小数点右移4位，尾数就是 1.1001 1001 ，指数 E = -4 +127 = 123 。

2.4、浮点数的精度是怎么回事？

计算机存储整数很简单，每个数字是确定的。但小数则不同，0到1之间的小数都无限种可能， 计算机有限的空间无法存储无限的小数 。因此计算机将小数也当成“离散”的值，就像整数那样，整数之间间隔始终为1。给小数一个间隔刻度，如下图，用钟表来举例，小数刻度（步进）为0.234（十进制）。

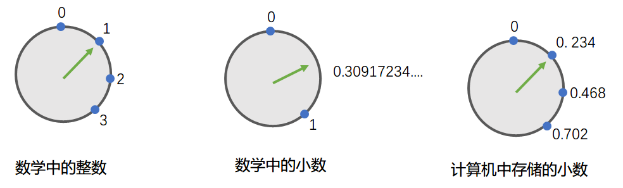
这样做的好处可以兼顾“所有”小数，小数的精度就取决于钟表的“刻度”，刻度越小，精度越高，当然存储时所需要的空间也就越大。

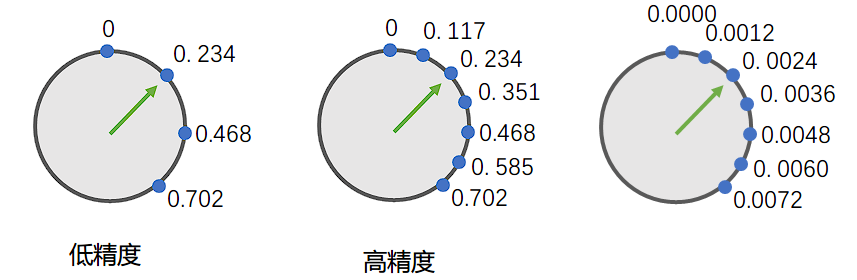
因此，这个精度本质上是由表盘间隔刻度（Gap）决定的，即使 0.0012 的间隔刻度，精度达到了4位十进制数，也只能保障前2~3位小数是可靠的。0.001X、0.002X、0.003X，他始终无法表示0.0013、0.0025。

可通过提高刻度（Gap）来提高精度，但存储长度是有限的，因此不管是那种浮点数都是有精度限制的。精度越高的数据类型，也需要更多的长度来存储数据。

32位 float 用了23位来存储有效数字，十进制也就6~7位（ 2^23=8388608 ）。在IEEE754规范中，小数的“刻度”并不是均匀分布的，而是越来越大，数值越大则精度越低。如下面的表盘和刻度尺的示意图，其精度（Gap）的分布是不均匀的， 0 附近数字的精度最高，然后精度就越来越低了，低到超过1。

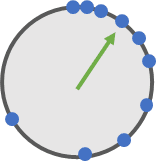
看看 float 的间隔刻度（Gap）如下图，来自官方 IEEE_754文档 ：

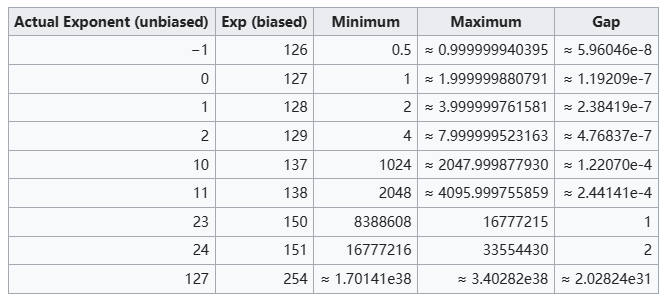
• 当数值大于8388608时，刻度（Gap）为1，就不能包含小数了。
• 当数字大于16777216（1600+万）时间隔刻度为2，连整数精度都不能保证了?。

//float大于8388608后的间隔为1
Console.WriteLine(8388608.1f == 8388608.4f); //True
//大于16777216后的间隔为2
Console.WriteLine(16777216f == 16777217f); //True
Console.WriteLine(16777218f == 16777219f); //False
Console.WriteLine(16777219f == 16777220f); //True

下图是double的刻度表：小于8的数字都能有16位精度。

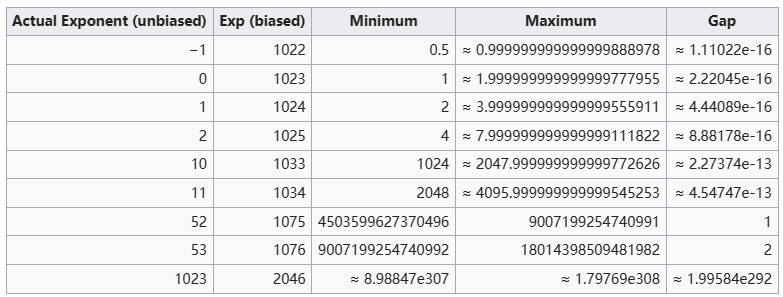
? 怎么感觉float很鸡肋呢？限制太多了！所以编程中浮点数多大都用的 double 居多，float比较少。

---

03、更精确的 Decimal

System.Decimal 是16字节（128位）的 高精度十进制浮点数 ，不同于float、double 的二进制存储机制，Decimal 采用10进制存储，表示-7.9E28 到 +7.9E28之间的十进制数。Decimal 最大限度地减少了因舍入而导致的错误，比较适用于对精度要求高场景，如财务计算。

? Decimal并不属于IEEE754规范，也不是处理器支持的类型，计算性能要差一点点（约 double 的 10%）。

Console.WriteLine(1f / 3f * 3f); //1
Console.WriteLine(0.1 + 0.2 == 0.3); //False
//decimal更高精度
Console.WriteLine(1m / 3m * 3m); //0.9999999999999999999999999999
Console.WriteLine(0.1m + 0.2m == 0.3m); //True

Decimal可以准确的表示 0.1 ，Decimal 128位的存储结构如下图（ 图来源 ）：

• 96位 存储一个大整数，就是有效数字， Math.Pow(2,96) = 7.9E28 ，最多28位有效数字，因此小数最多也就是28位（全是小数时）。
• 剩下的 32位 中，有一个符号位，0 表示正数，1 表示负数。其中有 5 位（下图中的第111位）表示10的指数部分（0到28的整数），可以理解为小数点的位置，其他位数没有使用默认为0（有点浪费呢？）。

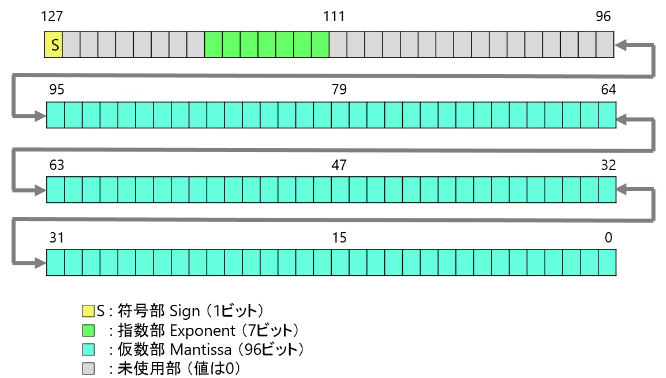
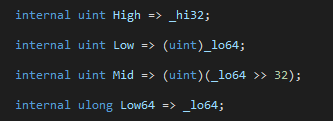
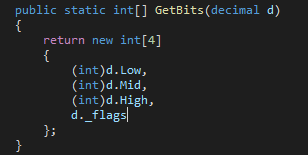
Decimal 表示小数其实是“障眼法”，内部有三个int （High、Mid、Low）来表示96位有效数字，还有一个int表示指数。可以通过 decimal.GetBits() 方法获取他们的值。下图来自 Decimal 源码 Decimal.cs

3.1、为什么Decimal没有0.1问题？

在Decimal中就没有 0.1+0.2 不等于 0.3 的问题，因为她能准确表示 0.1 。

其根本原因就是 Decimal 不会把小数转换为二进制，而是就用十进制。把小数都转为整数存储，如 0.1 在Decimal 中会被表示为 1* 10^-1 ，尾数为1，指数为 -1 ， 指数就是小数点位置 。

? Decimal值 =

var arr = decimal.GetBits(0.1M);	
Console.WriteLine($"尾数：{arr[2]}{arr[1]}{arr[0]}");
Console.WriteLine($"指数："+$"{arr[3]:B32}".Substring(0,16));
//尾数：001
//指数：0000000000000001

100.1024 存储为 1001024* 10^-4 。

• 尾数为 1001024 ，全都转换为整数了。不用担心超出整数int范围， 96 位有三个整数并行存储呢！
• 指数为 4 ，小数点位置在第四格。

var arr = decimal.GetBits(100.1024M);	
Console.WriteLine($"尾数：{arr[2]}{arr[1]}{arr[0]}");
Console.WriteLine($"指数："+$"{arr[3]:B32}".Substring(0,16));
//尾数：001001024
//指数：0000000000000100

如果是负数 -100.1024 ，则只有符号位为 1 ，其他一样

var arr = decimal.GetBits(-100.1024M);	
Console.WriteLine($"尾数：{arr[2]}{arr[1]}{arr[0]}");
Console.WriteLine($"指数："+$"{arr[3]:B32}".Substring(0,16));
//尾数：001001024
//指数：1000000000000100

? 所以 Decimal 值只要没有超过28~29位有效数字，就没有精度损失！是不是Very Nice！flaot、double 损失精度的根本原因是其存储机制，必须把小数转换为二进制值，再加上有限的精度位数。

3.2、Decimal、Double、Float对比

类型	单精度 float	双精度 double	Decimal 高精度 浮点数
类型	System.Single	System.Double	System.Decimal
规范	IEEE754	IEEE754	无，.Net自定义类型
是否基元类型	是	是	是
长度	32位（4字节）	64位（8字节）	128位（16字节）
内部表示	二进制，基数为2	二进制，基数为2	十进制，基数为10
字面量（后缀）	f / F	后缀 d / D	后缀 m / M
最大精度	6~7	15~16	28~29位
范围	±3.4E38 ， 2^23=3.4E38	范围很大，±1.7*E308	-2^(96) 到 2^(96)，±7.9E28
特殊值	+0、-0、+∞、-∞、NaN	+0、-0、+∞、-∞、NaN	无
速度	处理器原生支持，速度很快	处理器原生支持，速度很快	非原生支持，约 double 的 10%

Decimal 虽然精度高，但长度也大，计算速度较慢，所以还是根据实际场景选择。财务计算一般都用 Decimal 是因为他对精度要求较高，钱不能算错，传说算错了要从程序员工资里扣??。

---

04、一些编程实践

• 对于精度要求高的场景不适合用浮点数（double、float），推荐 decimal ，特别是价格、财务计算。
• 浮点数不适合直接相等比较，直接相等大多会出Bug。
• 在存储比较大的数字时，需注意float、double 对于整数也有精度问题。

4.1、浮点数的相等比较

• 使用相同的精度进行比较， Math.Round() 获取相同的精度值。
• 比较相似性，根据实际场景设定一个误差值，如 1e-8 ，只要差值在这个误差范围内，都认为相等。

var f1 = 0.1 + 0.2;
var f2 = 0.3;
	
Console.WriteLine(f1 == f2); //False
//相同精度
Console.WriteLine(Math.Round(f1,6) == Math.Round(f2,6)); //True
//误差范围
Console.WriteLine(Math.Abs(f1-f2)<1e-8); //True

4.2、取整与四舍五入

取整方式	说明/示例
整数相除 10/4=2	抛弃余数，只留整数部分
强制转换 (int)2.9=2	直接截断，只留整数部分，需要注意‼️
Convert转换，四舍五入取整	Convert.ToInt32(2.7) = 3; Convert.ToInt32(2.2) = 2;
格式化截断，四射五入	字符串格式化时的截断，都是四舍五入， $"{2.7:F0}" = "3"
Math.Ceiling() ，向上取整	Math.Ceiling(2.3) = 3 ，⁉️注意负数 Math.Ceiling(-2.3) = -2
Math.Floor() ，向下取整	Math.Floor(2.3) = 2 ，⁉️注意负数 Math.Floor(-2.3) = -3
Math.Truncate() ，截断取整	Math.Truncate(2.7) = 2 ，只保留整数部分，同强制转换
Math.Round() ，四舍五入	可指定四舍五入精度， Math.Round(2.77,1) = 2.8

---

参考资料

• MSDN： System.Decimal 结构
• MSDN： 浮点数值类型（C# 引用）
• IEEE 754-1985
• IEEE Floating-Point Representation
• IEEE-754 Floating Point Converter ，浮点数在线转换器
• IEEE-754 floating point numbers converter ，也是一个在线浮点数在线计算器
• IEEE754详解
• 都工作两年了，还不知道浮点数如何转二进制？

---

©️版权申明 ：版权所有@安木夕，本文内容仅供学习，欢迎指正、交流，转载请注明出处！ 原文编辑地址-语雀